Musings on Newcomb’s problem

Newcomb’s paradox posits a game with a transparent box containing $1 and an opaque box containing either $0 or $1,000. A Player is offered the choice between only the opaque box or both boxes. Before the Player makes this choice, a Predictor has attempted to predict the Player’s choice. The Predictor puts $1,000 into the opaque box, if the prediction is that only this box will be chosen. Otherwise, the Predictor puts $0.

The Predictor neither has a time machine nor some gift for backward causation. It is assumed, however, that the Predictor is rather reliable, though not necessarily infallible. Should the Player choose the opaque box only or both boxes?

Born to learn?

There’s a debate in linguistics on the extent to which humans acquire language via learning and statistical generalization and the extent to which language acquisition aided by innate biases. Theoretical arguments have been devised to demonstrate that general-purpose learning would require to much data and that innate bias is necessary. An eprint claims to provide mathematical and empirical support against such impossibility results and in favor of the possibility of language acquisition through general-purpose learning. The learning method being advanced is a Minimum Description Length type method.

A. S. Hsu, N. Chater and P. M. B. Vitanyi. The probabilistic analysis of language acquisition: Theoretical, computational, and experimental analysis. arXiv:1006.3271 (2010)

Causal sets (causets) and computation

A remarkable eprint just appeared: T. Bolognesi, Causal sets from simple models of computation, arXiv:1004.3128.

In the theory of relativity, the relation “event A happened before event B” is not a total ordering relation. When events have space-like separation, the relation “before” is observer-dependent. By restricting attention to a partial ordering relation, that only applies to pairs of events with time-like separation, an observer-independent relation is obtained.

The theory of relativity is concerned with continuous, smooth manifolds. Computation is usually conceived of in terms of a discretized state space. To connect some aspects of the two, the new eprints defines a partial ordering relation on computational events (e.g. state transitions in a Turing machine) that represents a “before” relation. The resulting visualizations of the partial ordering relations as graphs are intriguing. Whether or not one believes this sort of mathematical structure will have useful applications in physics, the eprint is worth a read just for its visualizations.

Shogenji’s new measure of Bayesian justification

Proponents of Bayesian epistemology have invented several different quantitative measures of how available evidence bears on different hypotheses. These measures are referred to as measures of evidential support, coherence, confirmation, or justification, depending a bit on the precise significance ascribed to them. Presently, Bayesians disagree over which of these measure is the most useful, but a new paper by Shogenji provides very appealing alternative measure and, with some luck, may even settle this debate.

At first sight, it might appear that the posterior probability 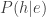of a hypothesis 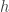conditional on observed evidence is the perfect measure for a Bayesian. However, a hypothesis sometimes has a high posterior probability simply by virtue of a high prior probability, without necessarily being support/confirmed/justified by virtue of the observed evidence.

Generic optimization in infinitely large search domains

In 1995 and the following few years, Wolpert and Macready published a technical reports and a journal article on what has come to be called the No Free Lunch theorems. These theorems say that all optimization algorithms yield the same average performance in optimizing a completely random function.

A condensed matter interpretation of the Standard Model

Condensed matter physics provides mathematical analogies with particle physics. Quasiparticles, i.e. particle-like excitations of a given ground state, often share many physical properties with more fundamental particles. Among the many attempts to find deeper insights into the Standard Model is the exportation of analogies in the other direction: from condensed-matter physics to fundamental physics. Here’s one such line of work:

I. Schmelzer. A condensed matter interpretation of SM fermions and gauge fields. arXiv:0908.0591

Abstract: We present the bundle Aff(3) x C x /(R^3), with a geometric Dirac equation on it, as a three-dimensional geometric interpretation of the SM fermions. Each C x /(R^3) describes an electroweak doublet. The Dirac equation has a doubler-free staggered spatial discretization on the lattice space Aff(3) x C (Z^3). This space allows a simple physical interpretation as a phase space of a lattice of cells in R^3. We find the SM SU(3)_c x SU(2)_L x U(1)_Y action on Aff(3) x C x /(R^3) to be a maximal anomaly-free special gauge action preserving E(3) symmetry and symplectic structure, which can be constructed using two simple types of gauge-like lattice fields: Wilson gauge fields and correction terms for lattice deformations. The lattice fermion fields we propose to quantize as low energy states of a canonical quantum theory with Z_2-degenerated vacuum state. We construct anticommuting fermion operators for the resulting Z_2-valued (spin) field theory. A metric theory of gravity compatible with this model is presented too.

A recent follow up paper focuses on neutrinos:

I. Schmelzer. Neutrinos as pseudo-acoustic ether phonons. arXiv:0912.3892

Abstract: Recently [arXiv:0908.0591] the author has proposed a condensed matter model which gives all fermions and gauge fields of the standard model of particle physics. In the model, the inertness of right-handed neutrinos is explained by an association with translational symmetry. We argue that this association may be used as well to explain the small neutrino masses. They appear to be pseudo-Goldstone particles associated with an approximate translational symmetry of a subsystem. Then we propose to explain the masslessness of SU(3)_c x U(1)_em with an unbroken SU(3)x U(1) gauge symmetry of the model. We also detect a violation of a necessary symmetry property in the lattice Dirac equation and present a fix for this problem.

Convex analysis and thermodynamics

A previous post briefly reviewed convex analysis. Here I’ll review the application of convexity in basic thermodynamics.

Equilibrium states

The concept of thermodynamic equilibrium is a generalization of mechanical equilibrium, where all forces and torques cancel each other. Informally, the idea is that a system in thermodynamic equilibrium has stable, unchanging macroscopic properties, which may be characterized by an n-tuple of extensive variables.

I, AIXI

A new cool eprint has appeared:

J. Veness, et al. A Monte Carlo AIXI Approximation. eprint: 0909.0801

The question that defines the context for this article is: How should probabilities be assigned? One way, with much to recommend itself, is take them to be algorithmic probabilities or universal priors. Suppose one has observed the first N values of a discrete time series, maybe a byte stream, and wishes to predict or make a bet about the next value. Is there a general probability measure appropriate for all cases that fit this abstract setting and, if so, which one?

Clusters and tree structure from genealogical data

Modern biology provides a wealth of interesting mathematical challenges in the modeling and reconstruction of evolution. A new eprint explores the theoretical prospects for defining a phylogenetic tree structure, despite complications like lateral gene transfer, hybdridization and the difference between gene and species trees:

A. Dress, et al. Species, Clusters and the ‘Tree of Life’: A graph-theoretic perspective. eprint: 0908.2885

Thermodynamics and statistical mechanics of self-gravitating systems

It is not uncommon among scientists to consider philosophy of science to be an uninteresting distraction from more important matters. When it comes to the foundations of thermodynamics and statistical mechanics, however, some philosophers have made genuinely useful contributions, doing an excellent job of summarizing the current situation and bringing clarity to the strengths and weaknesses of different foundations. Jos Uffink’s article on what, strictly speaking, is asserted by the second law of thermodynamics comes to mind—it has been well received by both philosophers and physicists. To specialists in the field, there may not be much new, but philosophers have at the very least managed to provide clear presentations of successes and problems to a potential wider audience of philosophers, physicists, and lay-men.

I’d like to highlight two preprints by Callender and Wallace, respectively, on the subject of thermodynamics of self-gravitating systems.